
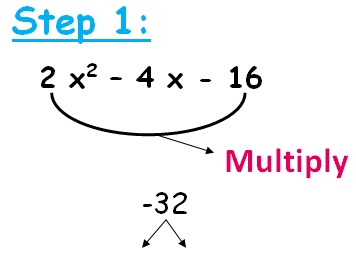
It will enable them to practice regularly in order to perform well in the exams. Students will be able to perform splitting the middle term and apply the quadratic formula efficiently. Benefits of Factoring Quadratics WorksheetĬuemath has created a set of factoring quadratics worksheets which will help students to get all of their doubts cleared. In this case, we have b 0 in the standard form of the quadratic equation, which gives us. Factoring quadratic worksheets by Cuemath covers both of them. Factoring Quadratic Binomials: Case 2 (b 0). Step 2: Replacing the values of a, b and c in the quadratic formula, we get: x b ± b 2 4 a c 2 a 4 ± 16 12 2 4 ± 2 2. Various methods are used in factorising quadratics, which mainly include splitting the middle term and the quadratic formula. In order to perform well in topics of algebra, factoring quadratics is one of the most primary concepts one must learn. This is one of the basic concepts one must be thorough with, to proceed further in mathematics. The GCF is 2x, so factor a 2x fr0m the expression:įind two numbers that multiply to get -24 and then add to get to 10.Learning the concept of factoring quadratics is very important from a mathematics point of view. This equation is already in the proper form where a. In this case, find the greatest common factor of both terms: Factoring Quadratic Equations when a 1 Step 1: Write the equation in the general form. In the same way, factoring can be difficult unless you know the concept behind it.įind 2 numbers that added together get to 5 and then multiply to get 6. You may wish to refer to Chapter 0 to review prerequisite skills. To get ready, identify important terms and organize your resources. If factoring is hard, the quadratic formula (a shortcut for completing the square) helps. 470 Chapter 8 Factoring and Quadratic Equations Get Started on Chapter 8 You will learn several new concepts, skills, and vocabulary terms as you study Chapter 8. Indeed, the basic principle to be used is: if a and b are real or. Graphing gives a good visual, but it is hard to find values of x from a graph with no equation. Sometimes it is easier to find solutions or roots of a quadratic equation by factoring.
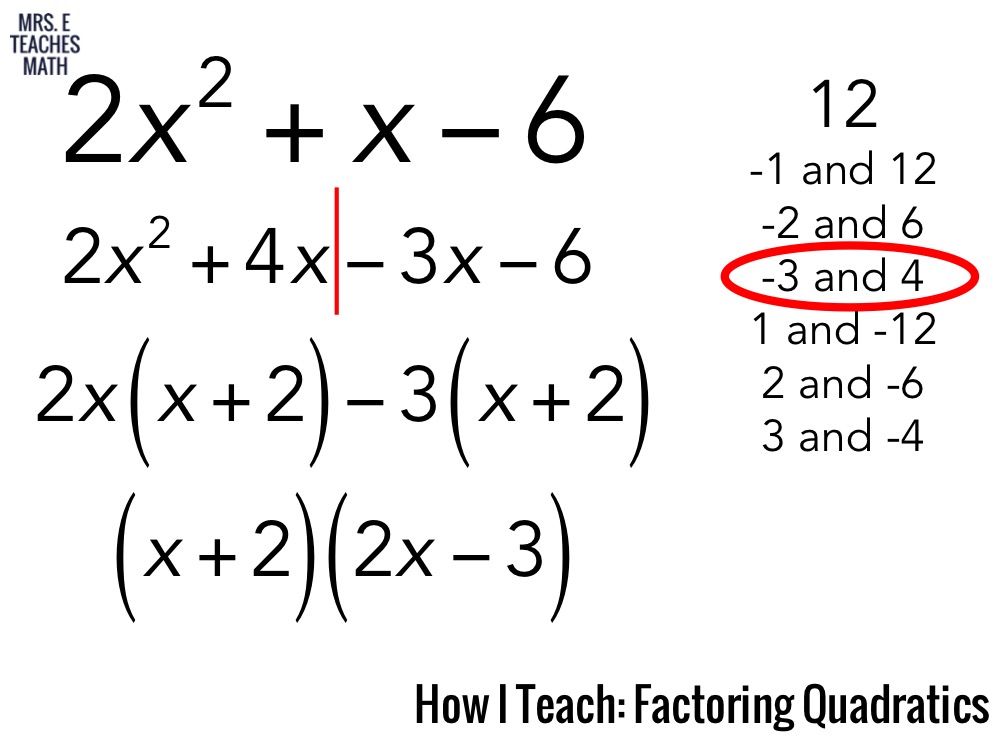
Factoring quadratic equations how to#
It is EXTREMELY important that you understand how to factor trinomials in order to complete this lesson. If the equation can be factored, then this method is a quick and easy way to arrive at the solution. There are several different ways to solve a quadratic equation.

Remember expanding an equation and factoring are totally different – where expanding is quite simple, factoring is difficult – it’s as if you want to find the ingredients of a tasty pizza after it was delivered. You can solve quadratic equations by graphing, factoring, completing the square, & the quadratic formula. By factoring quadratic equations, we will be able to solve the equation. If factoring a quadratic equation is all about finding factors, then we need to determine the factors, or a factor, that that we multiply by.īecause when you multiply these factors you get: Search: Modeling Quadratic Functions Worksheet. Let’s explain this concept, if factoring quadratic equations, with a simple example: Also, note that we now know that we must avoid w 2 w 2 so we. This is an equation containing rational expressions so we know that the first step is to clear out the denominator by multiplying by the LCD, which is w + 2 w + 2 in this case. Use factoring to solve the following equation. The quadratic equation x 2 7x + 10 0 has roots of x 2 and x 5. They can be: real and distinct real and equal imaginary (complex) Example 1. All quadratic equations have 2 solutions (ie.

In other words, we call it factoring, only because we are finding the factors of the quadratic equation. Section 2-5 : Quadratic Equations - Part I. The solution of an equation consists of all numbers (roots) which make the equation true. A quadratic equation can be easily solved, applying algebra rules along with applying all the factoring methods. Simply put, a quadratic is nothing but a polynomial that looks like “ax 2 + bx +c” where all a, b and c are a number, but the important thing is either b and c can be 0, but can never be a zero.


 0 kommentar(er)
0 kommentar(er)
